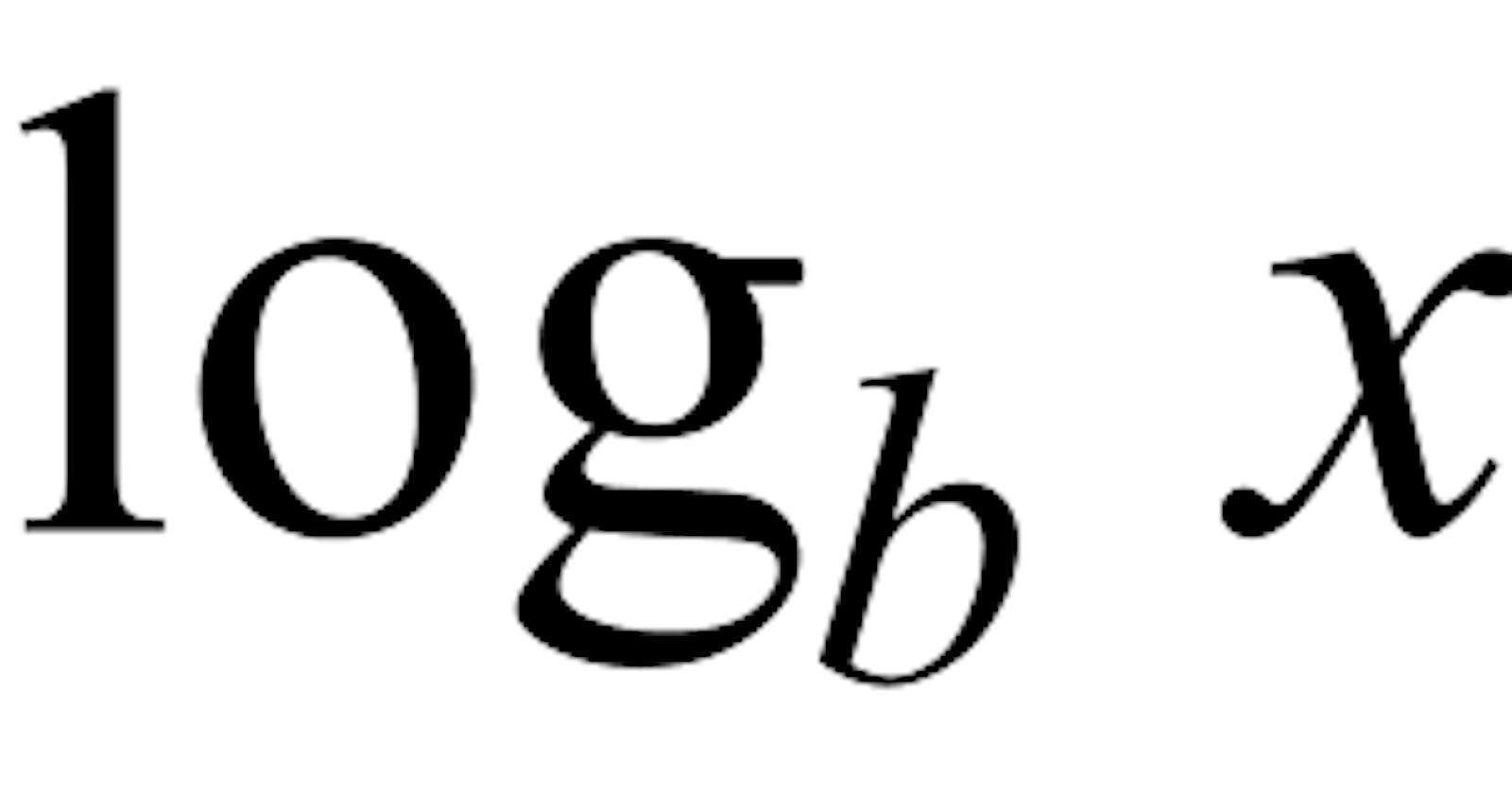What does O(logN) mean in big O notation?

For a lot of people, some topics in computer science are intimidating because they are closely related to mathematics. Complexity Analysis is one of these topics.

For the most part, we can try to understand this topic - $O(1)$ indicates that the algorithm runs in constant time, right? And $O(N)$ means it runs in linear time. Enter $O(log N)$; you guessed right, I am out the door! But it doesn’t have to be this way.

In this article, we will discuss the “scariest” of them all, $O(log N)$. First, by looking at its mathematics, how it works and then examining how it relates to Complexity Analysis and Computer Science.

Prerequisites

To follow along in this article, you need to have a basic knowledge of some math concepts (I know, I know, it gets better, I promise.), which I have provided some explanations and references for below;

Exponent: This refers to how many times a number is multiplied by itself. For example, $8^2$ means 2 is an exponent of 8. This results in 64 because 8 * 8 = 64.
Inverse function: A function's inverse function undoes the function's operation.
Logarithm base: In Logarithm, you have to specify a base. In mathematics, it is typical to assume that the base number is 10. But this base number, $b$, could honestly be anything. In computer science, we assume it to be base-2 i.e., binary logarithm. We make this assumption because we assume we are dealing with binary operations. You may have noticed that the big O notation $O(log N)$ has no base number visually represented. This is because of the above assumptions.
Binary numeral system: A system of maths expressions with only zeros and ones.

What is Logarithm?

Wikipedia defines logarithm as the inverse function of exponentiation. This means that the result of finding the logarithm of a number, say $N$ is the exact amount, which its base number, say $b$, must be raised to get $N$. For example, in a binary logarithm(base-2) system, $logN$ is the exponent of 2 that results in $N$., i.e., the power you need to put 2 to to get $N$. Such that;

$$log_2N = y$$ If and only if; $$2^y = N$$

Okay, okay! Now, what does this mean for simple software engineers like us?

Complexity Analysis & Big O Notation

Complexity analysis allows us to compare two or more algorithms and decide which is the “better” algorithm simply by looking at how long it takes each to complete and how much space is consumed in the process given $N$ number of inputs. $N$ could be anything. It could be 1 billion!

In response to your question above (or the one I asked for you 😁), this means a lot to us. As engineers, we portray complexity analysis using something called the Big O notation. And what is that? You may ask. Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. There are a couple of these, and we use them to describe the complexity analysis of algorithms. Notable Big Os include;

$O(1)$ - Constant time
$O(log N)$ - Logarithmic time
$O(N)$ - Linear time
$O(N logN)$ - Log-linear time
$O(N^2)$ - Linear-square time
$O(N!)$ - Factorial time

You may have begun to realize why logarithms and all the other jargons above matter to us now huh 😅. You’re welcome 😊! It gets better. Logarithmic time complexity is the second-best complexity an algorithm can have, and it comes only after constant time complexity. Let’s put this in context;

From the information above, we know that log of N is the power to which 2 has to be raised to get N ($log_2N= y$ if and only if $2y = N )$. This means that;

when $N = 1$, $y = 0$ because $2^0 = 1$

when $N = 2$, $y = 1$ because $2^1 = 2$

when $N = 4$, $y = 2$ because $2^2 = 4$

when $N = 8$, $y=3$ because $2^3 = 8$

when $N = 16$, $y=4$ because $2^4 = 16$

when $N = 32$, $y=5$ because $2^5 = 32$

A quick observation of the above brings to light a pattern. Whenever we doubled the input($N$), the algorithm’s complexity($y$) increased by 1. Pretty Cool, right? This is how exponents of the number 2 work; increasing the exponent by 1, doubles the resulting value. This is great for an algorithm because this implies that if the inputted values double, the algorithm only needs to take one additional computational step.

That said, the above may still seem a bit trivial, especially for us engineers; I mean, what is the difference between 16 and 32? It’s not that big of a deal 🤪, right? Let’s look at two more example inputs below;

when $N = 1,000,000$, $y ≅ 20$ because $2^{19.93156857} ≅1,000,000.00$

when $N = 1,000,000,000$, $y ≅ 30$ because $2^{29.8974} ≅1,000,032,679.66$

Note: $≅$ symbolizes approximation

Yes, it’s exactly what you think it is, we moved from a million inputs to a billion inputs, and we only had to perform less than 10 additional operations. It doesn’t seem much with smaller numbers, but the essence becomes clearer with larger numbers. This is depicted in the chart below;

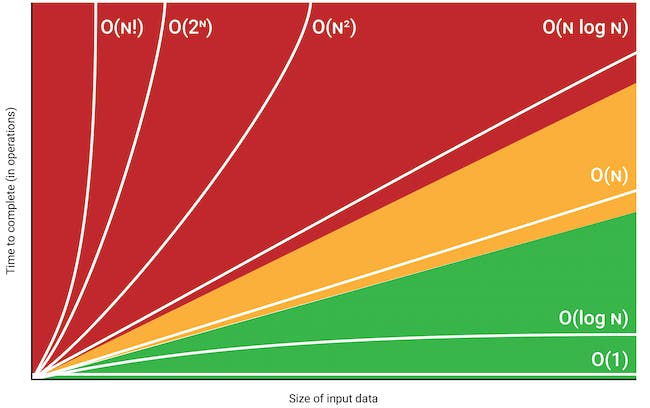
In this image of the Big O chart above, we can see that the $O(log N)$ line starts to increase rapidly with smaller input sizes, but as it tends towards the larger input sizes, It doesn't even appear to be increasing visually.

So next time you find yourself wondering if your algorithm has a time complexity of $O(log N)$, ask yourself, does doubling my input only require an additional computational step? If yes, it’s probably an $O(log N)$ algorithm.

The Famous Binary Search Algorithm

The Binary Search Algorithm is arguably the most popular algorithm when discussing this topic, and for valid reasons. It is the perfect example of an algorithm where doubling the input size increases time complexity by 1. Let us spend some time analyzing this algorithm to learn more about Logarithms in complexity analysis.

Binary Search Algorithm steps

The binary search algorithm starts with a sorted list, which is required as it is the only way it works.

/* Say we are given this sorted list => [2, 3, 5, 16, 19, 26, 34, 60, 128] */
/* And we have to search for an integer => 5 */

1) We’ll then keep track of the first and last values in the list by creating variables for them.

/* first is 2 */
/* last is 128 */

2) Then we will check the middle value in the list to see if it’s greater than or less than the target value(the value that is being searched in the list).

/* middle is 19 */

3) If the middle value is less than the target value, we can eliminate the left half of the list and update the first and middle values.

/* 19 is the middle number, and it is not less than 5 (the target number), so we don’t need to do the above here */

4) If the middle value is greater, we can eliminate the entire right side and update the last and middle values.

/* 19 is greater than 5, so we can eliminate the right side of the list.
* the searchable area of the list is now [2, 3, 5, 16, 19] 
* the last value is now 19 
* the middle value is now 5, which, lucky for us, is the target value.*/

We do these eliminations because we know that there’s no way we could find our missing value amongst these values.

5) This process is repeated until we find the target value or the left and right values overlap, indicating that the target value is not on the list.

We can observe how this approach to search completely ignores huge chunks of data just by knowing for certain that the missing value couldn’t be found within them.

If we were to double the size of this list like below;

/* new list => [2, 3, 5, 16, 19, 26, 34, 60, 128, 150, 156, 170, 179, 180, 199, 200, 220, 223] */

We will only need to do one additional step of eliminating the just added half if we are still searching for the target number of 5.

Let’s wrap this up by taking a look at an actual implementation of this algorithm using TypeScript;

function binarySearch(sortedList: number[], target: number): boolean {
        // initial first and last values
    let first = 0;
    let last = sortedList.length;

    do {
    // calculates the index of the middle Value
        const middleValue = Math.floor(first + (last - first) / 2);

    // the current middle value
        const value = sortedList[middleValue];

        if (target === value) {
    // if the target is the current middle value, return true
    // indicating we found it
            return true;
        } else if (value > target) {
    // if the current middle value is greater than the target
    // update the last value
            last = middleValue;
        } else {
    // else if the current middle value is less than the target
    // update the first value
            first = middleValue + 1;
        }
    // will run until both values overlap
    } while (first < last);

    return false;
}

In conclusion

$log_2(N)$ is the exponent of 2 that results in $N$.
Complexity Analysis helps us to decide which algorithm is “better” based on the number of operations and space consumed given an input size($N$).
Big O Notation is how we describe the complexity of an algorithm.
An algorithm has a complexity of $O(log N)$ if doubling its input results in one additional computational step.

Logarithm in Complexity Analysis Explained

Table of contents